Jaký je účiník transformátoru?

Účiník je určen vztahem cosφ₁=P₁/S₁=P₁/ , kde: P₁,Q₁, S₁ – činný, jalový a celkový výkon motoru.

Р₁ = P₂ + ∆P, kde: P₂ – výkon na hřídeli (čistý výkon); ∆P – ztrátový výkon. ∆P = ∆P_E + ∆P_umění. + ∆_Srst,

kde: ∆P_E – elektrické ztráty (ztráty způsobené ohřevem vinutí); ∆P_umění. – ztráty v oceli (ztráty způsobené ohřevem aktivní zóny);

∆P_srst – mechanické ztráty. Elektrické ztráty ∆P_E závisí na proudech ve vinutí a zvyšují se s rostoucím zatížením hřídele. Ztráty v oceli nezávisí na zatížení hřídele, ale závisí na napětí aplikovaném na vinutí statoru. Mechanické ztráty se týkají trvalých ztrát. V nominálním režimu je cosφн = 0,75÷0,95, cosφхх = 0,08÷0,15.

Pokles cosφхх se vysvětluje tím, že činný výkon je nízký (P_1xx = ∆P_E + ∆P_umění. + ∆P_srst) a jalový výkon Q₁ zůstává stejný jako v nominálním režimu. Na Obr. Obrázek 2.28 ukazuje závislost účiníku asynchronního motoru na zatížení hřídele. Když je asynchronní motor silně zatížen, má nízký účiník, což je ekonomicky nerentabilní.

Pro zvýšení cosφ při nízkém zatížení se doporučuje snížit napětí dodávané do motoru. Současně se snižuje jalový výkon a zvyšuje se účiník.

Vstupenka 6. Komplexní číslo, jehož modul a argument jsou amplituda a počáteční fáze syn. proud se nazývá komplexní proudová amplituda:.

2. Vnější charakteristika transformátoru se nazývá závislost sekundárního napětí na zatěžovacím proudu při konstantních hodnotách primárního napětí a účiníku zátěže: U₂‘= f(I₂‘) nebo U₂= f(I₂) v U₁ =U_1nom = konst a cosφ₂ = konst.

Když je transformátor naprázdno, můžeme předpokládat, že U₂‘=U₂₀‘=U₁, takže ty’₂ = U’₂₀ – ΔU, tj. napětí na sekundárním vinutí se od napětí naprázdno liší o hodnotu úbytku napětí v transformátoru. Pro poslední rovnici máme (%): U’₂ =U₂ = 100 – ΔU.

Pro vysokovýkonné transformátory (%): U₂ = 100 – βU_ksinφ₂. (7.20)

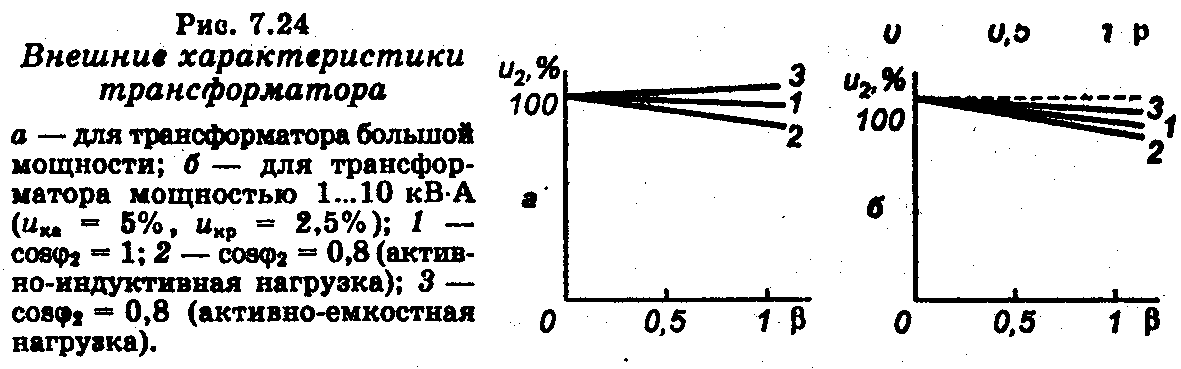
Na Obr. 7.24a ukazuje vnější charakteristiky transformátoru pro několik hodnot cosφ₂. Ve výkonových transformátorech při cosφ₂ = 1 bude sinφ₂ = 0 a napětí U₂ zůstává nezměněn při všech hodnotách zatížení. S aktivní indukční zátěží φ₂ kladné a čím větší je, tím větší je ztráta napětí a tím větší je snížení napětí U₂ se zvyšujícím se zatěžovacím proudem. S aktivní kapacitní zátěží φ₂ záporná a napěťová ztráta ΔU= – βU_ksinφ₂ také negativní. Rovnice (7.20) se změní na U₂ = 100 + βU_ksinφ₂ , z čehož vyplývá, že s rostoucím β, tedy s rostoucím zatěžovacím proudem, napětí U₂ zvyšuje ve srovnání s U₂₀. U transformátorů malého výkonu nelze opomenout činnou složku napětí nakrátko. V tomto případě, abyste určili ztrátu napětí, musíte použít rovnici, ve které jsou všechny pojmy vyjádřeny v procentech: U₂ = 100 – β(U_kacos₂ +u_crsinφ₂).

Přítomnost U složky_ka způsobí pokles napětí U₂ při aktivní zátěži (cosφ₂ = 1) a snížení odchylky napětí od jmenovité hodnoty za přítomnosti jalové složky zatěžovacího proudu (indukční i kapacitní). Vnější charakteristiky transformátorů jsou téměř rovné. Pokles napětí při jmenovité zátěži velmi závisí na účiníku zátěže a napětí nakrátko, ale nemůže překročit hodnotu U_к.

Schémata zapojení pro třífázová vinutí.Primární a sekundární vinutí třífázových transformátorů (skupinové a tříramenné) jsou spojeny hvězdou nebo trojúhelníkem. V některých případech jsou vinutí transformátoru zapojena cik-cak. Při připojení vinutí do hvězdy na svorku nulového bodu je toto zapojení označeno znakem Y-. Schémata zapojení primárního a sekundárního vinutí transformátoru se dvěma vinutími jsou označena zlomkem, jehož čitatel udává schéma zapojení primárního vinutí a jmenovatel udává schéma zapojení sekundárního vinutí, například Y/ Y-, A/A, Y-/A. Schémata zapojení vinutí třívinutých transformátorů jsou označena následovně: Y/Y/Δ. Z ekonomického hlediska je výhodnější spojit vinutí transformátoru s vyšším napětím do hvězdy, protože pro získání daného síťového napětí U_л fázové napětí U potřebné_ф =U_л /, a tím i menší počet závitů vinutí a nižší spotřeba izolačních materiálů. Vinutí zapojené do trojúhelníku má také své výhody. Proud naprázdno je nesinusový. Když jsou vinutí spojena hvězdou bez nulového vodiče, neexistují žádné harmonické třetího řádu, které jsou ve fázi ve všech fázových proudech naprázdno. To vede ke zkreslení magnetických toků a výskytu harmonických EMF třetího řádu. Napětí sekundárního vinutí se stává nesinusovým. Pokud je vinutí spojené trojúhelníkem, pod vlivem EMF třetího řádu se v uzavřeném trojúhelníku vinutí objeví proud a pokles napětí ve vinutí vyrovná třetí harmonickou EMF. Lineární napětí vinutí zapojeného do trojúhelníku bude sinusové. Proto je u výkonových transformátorů jedno z vinutí obvykle zapojeno do trojúhelníku. Schémata zapojení vinutí transformátoru na elektrických obvodech jsou na Obr. 7.28. Začátky a konce vinutí primární fáze jsou označeny velkými písmeny (A, B, C a X, Y, Z) a začátky a konce vinutí sekundární fáze jsou označeny malými písmeny (a, b, c a x, y, z).

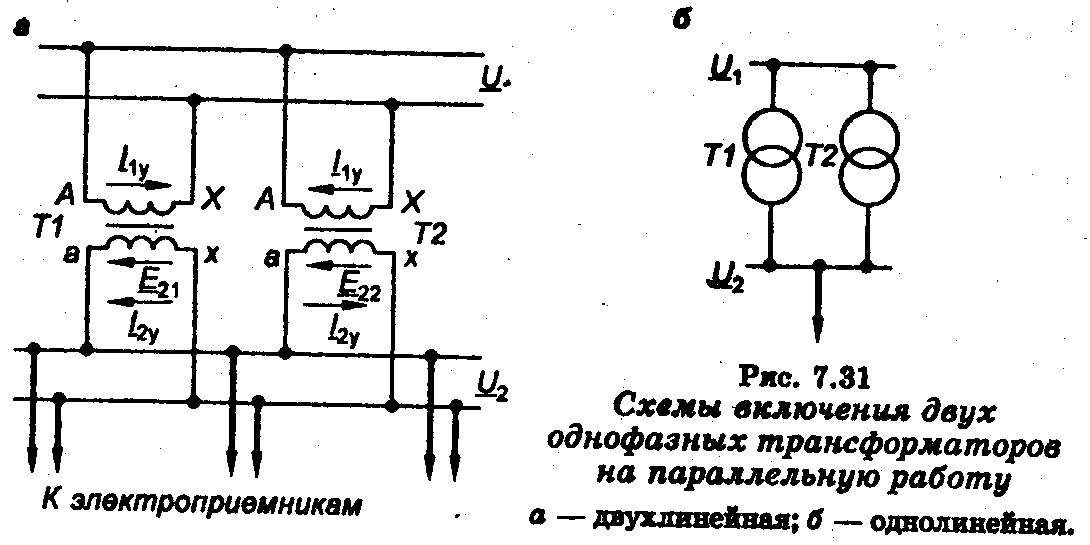
Paralelní provoz potrubí. Za určitých podmínek se může ukázat, že výkon jednoho transformátoru nestačí k napájení elektrického přijímače, pak se použijí dva nebo více paralelně zapojených transformátorů. Tato situace vzniká, je-li celkový výkon přijímačů připojených na sekundární vinutí transformátoru větší než výkon transformátoru nebo je-li vyžadována větší spolehlivost napájení přijímačů, kterou nezajišťuje jediný transformátor. Ve velkých energetických soustavách přenášejí elektřinu vysokonapěťová přenosová vedení, jejichž výkon nejčastěji převyšuje výkon jednoho transformátoru a na takovém vedení pracuje několik transformátorů.

V takových případech se transformátory zapojují paralelně (obr. 7.31). Při paralelním provozu jsou primární vinutí všech transformátorů (dvou nebo více) napájena stejným napětím U±. Sekundární vinutí všech transformátorů jsou připojena na stejné společné přípojnice, na které je připojena zátěž. Pro normální provoz v režimu paralelního připojení musí transformátory splňovat následující podmínky:

1) transformační poměry všech transformátorů musí být stejné, tj₁ = k₂ = k₃ = . = k_n;

2) zkratová napětí všech transformátorů musí být stejná, tj. u_k1=u_k2=u_k3=…=u_kn ;

3) třífázové transformátory musí mít stejnou skupinu připojení vinutí.

Protože primární vinutí transformátorů jsou připojena k jednomu zdroji s napětím U₁, pak při volnoběhu, aby byla sekundární napětí všech transformátorů stejná, je nutné, aby jejich sekundární EMF byly stejné. K tomu dochází pouze tehdy, když jsou transformační koeficienty stejné. Pokud má transformátor T1 (obr. 7.31a) vyšší transformační poměr než transformátor T2, pak E₂₁ > E₂₂. V uzavřeném obvodu sekundárních vinutí transformátorů pod vlivem EMF ΔE₂ = E₂₁ – E₂₂ ≠ 0 bude existovat vyrovnávací proud I_2y, které se přemění na primární vinutí. Hodnota tohoto proudu závisí také na odporu vinutí transformátoru a fáze proudu závisí na složkách impedancí transformátoru (obr. 7.32). Vyrovnávací proud ve vinutí není proud zátěže, ohřívá vinutí a

snižuje užitečný výkon transformátoru. Pro praxi se považuje za přijatelné odchylky hodnot transformačních koeficientů od sebe o 0,5 %.

V režimu zatížení sekundární napětí U₂ každý transformátor závisí na jeho vnějších charakteristikách (obr. 7.33). V tomto případě odchylka napětí U₂ od napětí naprázdno U₂₀. stejné pro všechny paralelně pracující transformátory, úměrné zkratovému napětí U_к transformátor. Pokud mají transformátory různá napětí U_к, pak bude sklon jejich vnějších charakteristik odlišný. Na Obr. 7.33 uvádí vnější charakteristiky transformátorů, pro které U_k2 > U_k1.

Protože sekundární vinutí obou transformátorů jsou připojena ke společným sběrnicím, budou napětí na jejich sekundárních vinutích vždy stejná a rovna napětí na sběrnicích U_2ш. Při určité zátěži napětí U_2ш bude mít hodnotu odpovídající přerušované čáře na obr. 7.33, jejichž průsečíky s vnějšími charakteristikami transformátorů jsou pracovními body pro daný režim. Úsečky těchto bodů určují zatěžovací proud každého transformátoru a I₂₂ 21.

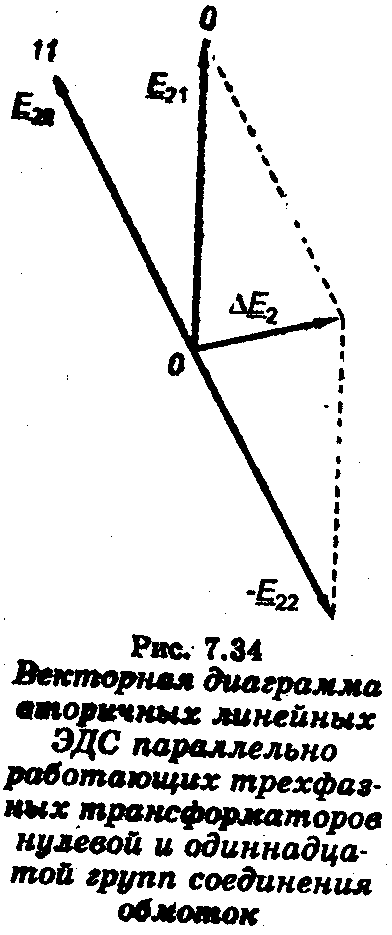
Tedy transformátory s různým U_к zatížené jinak: transformátor s menšími a_к zatížené větším proudem než transformátor s velkým U_к. S rostoucím výkonem přijímačů se zvyšuje zatížení obou transformátorů. Když však zatížení transformátoru T1 dosáhne jmenovité hodnoty, bude zatížení transformátoru T2 stále daleko od jmenovité hodnoty. Plný výkon transformátoru T2 nelze využít, protože transformátor T1 bude přetížen. Proto musí mít transformátory zapojené pro paralelní provoz stejné hodnoty U_к. Je povolena odchylka od aritmetického průměru maximálně ±10% Třetí podmínka je naprosto přísná. Pokud transformátory patří do různých skupin připojení vinutí, pak se fázový posun mezi vektory lineárního sekundárního EMF (a tedy napětí) bude lišit od 0° a jejich vektorový rozdíl nebude roven nule. Na Obr. Obrázek 7.34 ukazuje vektorový diagram lineárních sekundárních EMF transformátorů patřících do skupiny připojení nula a jedenáctého vinutí. Výsledné emf ΔE₂=E₂₁ – E₂₂ tak velký, že vyrovnávací proud, který vytváří, několikrát překročí jmenovitý proud a režim se ukáže jako nouzový.

3. Závislost elektromagnetického momentu na skluzu: M=3I₂ 2 R₂/(SΩ₁), kde M – el/mag. moment, já₂ – proud rotoru, S – skluz, Ω₁ – úhlová rychlost rotace pole.

Závislost proudu rotoru na S: Pod vlivem rotoru EMF E_2Sindukovaný rotujícím magnetickým polem se v uzavřeném vinutí rotoru objeví proud I₂, určeno Ohmovým zákonem: (12.12)

kde R₂ — aktivní odpor fáze rotoru; Z_2S – fázová impedance rotoru.

Aktuální I₂ ve vinutí rotoru má stejnou frekvenci f₂=sf, stejně jako emf E_2S. Protože impedance fáze rotoru má indukční složku X_2S, pak aktuální I₂ zaostává ve fázi od E_2S podle úhlu ψ₂=arctg(X_2S/R₂) (12.13).

Při kritickém skluzu dosáhne moment stroje své maximální hodnoty: . Skluz, při kterém je moment roven maximu, lze nalézt tak, že vezmeme derivaci M a S a dáme jim rovnítko: S_cr= ±(R₂/X₂₀).

Z grafů a vzorců je zřejmé, že:

1) AM může pracovat v režimu motoru i generátoru v závislosti na skluzu;

2) AM pracuje stabilně při hodnotách skluzu

3) číselná hodnota S_cr je určeno hlavně parametry rotoru, měnící se R₂ můžeme zvýšit nebo snížit S_cr.

Otázka 1. Rezonance v obvodu je dosažena při úhlové frekvenci W=1/(LC), proto se při připojení odporového kondenzátoru R na svorky frekvence nezmění.