Jak bude ukázáno později, střídavý odpor bude větší než stejnosměrný odpor kvůli nerovnoměrnému rozložení proudu v drátu a ztrátě energie do okolí. Proto na rozdíl od stejnosměrného odporu odpor r v obvodu střídavého proudu se nazývá aktivní.
Podle Ohmova zákona je napětí aplikované na prvek r v kterémkoli okamžiku, je určen výrazem . Odtud okamžitý proud, kde – amplituda proudu.
Efektivní napětí U a aktuální I menší hodnoty amplitudy faktorem; proto je efektivní proud, tj. roven efektivnímu napětí dělenému aktivním odporem.
Veličina měřená v jednotkách odporu a označená , tzv. kapacitní řetězy: .
Kapacita je nepřímo úměrná frekvenci použitého napětí.
Na základě výrazu (2-17) je určen vztah mezi efektivním napětím a proudem:
Hodnota se měří v jednotkách odporu a nazývá se indukční reaktance řetězy. Indukční reaktance je úměrná frekvenci.
Odpor obvodu určený vzorcem se nazývá celkový odpor obvodu. Reaktance se nazývá odpor Pokud v obvodu převládá indukční reaktance, je reaktance vyjádřena kladným číslem, fázový rozdíl mezi napětím a proudem je kladný (> 0) a napětí obvodu předbíhá proud. Pokud v obvodu dominuje kapacita, je reaktance vyjádřena záporným číslem, fázový rozdíl je záporný (< 0) a proud obvodu vede k napětí.

Průměrný výkon za periodu, stejně jako výkon stejnosměrného obvodu, určuje energii dodanou do obvodu za jednu sekundu. Proto jí říkají aktivní Napájení. Hodnota výkonu závisí na proudu a napětí obvodu a na fázovém úhlu mezi napětím a proudem. Násobitel se nazývá součiniteljehosilový prvek.
Proměnný výkon používaný ke zvýšení magnetických nebo elektrických polí nebo přiváděný zpět do sítě se nazývá reaktivní síla. Jeho amplituda. Vyjadřuje se jalový výkon ve voltampérech.
Výkon, který se mění s dvojnásobnou frekvencí a má amplitudu, se nazývá plná síla.
Trojúhelník odpor. Délky stran odporového trojúhelníku určíme vydělením odpovídajících napětí hodnotou proudu. Přepona odporového trojúhelníku představuje celkový odpor obvodu, nohy představují aktivní a reaktivní odpor. Když je >0 strana trojúhelníku jx směřující do levé části nohy r – převažuje indukční reaktance; na –jx směrováno doprava – převažuje kapacita.

Sériové zapojení aktivního odporu a induktoru. Diagram, rovnice napětí, trojúhelník napětí. Diagram.
Sériové zapojení aktivních a kapacitních odporů. Schéma, trojúhelník napětí. Diagram.
Sériové zapojení aktivních, kapacitních a aktivních indukčních odporů. Druhý Kirchhoffův zákon pro napětí. Systém. Vektorový diagram.
Napěťová rezonance. Podmínky pro získání napěťové rezonance. Celkový odpor, účiník, proud a výkon při napěťové rezonanci.
Indukční a kapacitní reaktance obvodu střídavého proudu se mohou navzájem zcela vyrovnat. V tomto případě máme v obvodu rezonanci. Při rezonanci je odpor obvodu čistě aktivní, úhel posunu mezi napětím a proudem je nula a = 1.
Rezonanci v obvodu lze dosáhnout třemi způsoby: změnou frekvence napětí obvodu, indukčnosti nebo kapacity nebo obojího.
Úhlová frekvence, při které dochází k rezonanci, se nazývá rezonanční nebo přirozená úhlová frekvence řetězy.
Rezonance zdůrazňuje. Při rezonančním napětí v obvodu Obr. 2–35, в napětí na tlumivce a kondenzátoru se vzájemně kompenzují a rezonanční úhlová frekvence je určena z podmínky kde.

Celkový odpor obvodu se vzájemnou kompenzací je roven pouze činnému odporu obvodu; tedy při konstantním napětí na svorkách U proud v obvodu dosáhne nejvyšší možné hodnoty. Napětí na svorkách cívky a kondenzátoru může desítkykrát převýšit napětí na svorkách obvodu. Proto rezonance při zapojení prvků do série se nazývá napěťová rezonanceиy.
Rovnost napětí, i když jsou fázově posunuta o 180°, znamená, že v každém okamžiku mají indukční a kapacitní napětí stejnou hodnotu a opačné znaménko: = – Výsledkem je, že okamžité hodnoty jalových výkonů odpovídají indukčnost a kapacita jsou stejné a mají opačná znaménka.
Zvýšení nebo snížení energie magnetického pole se rovná snížení nebo zvýšení energie elektrického pole, to znamená, že v obvodu probíhá nepřetržitá výměna energie mezi cívkou a kondenzátorem v důsledku změn napětí a proudu. a energie přicházející ze sítě pokryje energetické ztráty v ekvivalentním odporovém prvku s aktivním odporem.
Z výrazů pro kapacitní a indukční reaktanci při rezonanci získáme
hodnota Z rovný poměru nebo proudu I se měří v jednotkách odporu a nazývá se mávatвom odpor.
Závislost proudu v obvodu na frekvenci při konstantním napětí U na svorkách je znázorněno na Obr. 2-37. Křivka má maximum při , když je odpor obvodu nejnižší: . Na frekvenci dominuje kapacita a proud vede napětí; pro úhel a pro proudové zpoždění za napětím.

Paralelní zapojení odporů v obvodu střídavého proudu. Schéma zapojení, celkový proud a fázový posun mezi proudem a napětím v každé větvi obvodu. Trojúhelník proudů. Aktivní, jalový a zdánlivý výkon. Vektorový diagram.
Prozkoumejme obvod s paralelním zapojením odporového prvku, ideální tlumivky a kondenzátoru. Ve skutečnosti má každý induktor odpor a v kondenzátorech dochází ke ztrátám energie. Proto po zvážení idealizovaného obvodu, pro který se nejjednodušeji určí potřebné výrazy, budeme zkoumat obvody s reálnými prvky.
Když je přiloženo napětí, proud teče v nerozvětvené části obvodu
, kde jsou okamžité hodnoty činných, jalových indukčních a jalových kapacitních proudů.
Jalová složka proudů bude určena jako .
Proudy a v každém časovém okamžiku mají různé směry; znázorněno na Obr. 2-25 podmíněných kladných směrů lze zpočátku přiřadit identických, což odpovídá sčítání proudů. Vytvořme vektorový diagram a aktuální trojúhelník (Obrázek 2-26). Nohy proudového trojúhelníku jsou aktivní a jalové proudy, přepona pravoúhlého trojúhelníku proudů je proud I.
Vektor znázorňující jalovou složku proudu je nasměrován vpravo na (obr. 2-26, a) nebo doleva na (obr. 2-26,6) od vektoru napětí. Aktivní složka proudu má pro všechny hodnoty stejné znaménko. Reaktivní složka proudu mění znaménko spolu se změnou znaménka úhlu.

Proudový vektor rozvětveného obvodu je geometrickým součtem proudů jednotlivých větví.
Činné a jalové výkony jsou součtem výkonů jednotlivých větví:
Komplexní proud nerozvětvené části obvodu se rovná součtu komplexních proudů jednotlivých větví:
Komplexní proudy obvodu a větví jsou určeny produkty komplexního napětí a vodivosti:
Aktivní prvkyи jsou zdroje elektrické energie. Jsou rozděleny na zdroje napětí – symbol na obrázku.
Pasivní prvky – prvky, které nejsou zdroji elektrické energie. Dělí se na disipativní a reaktivní.
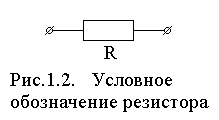
Disipativní prvky – prvky, které provádějí disipaci (disipaci) elektrické energie. Prvky s takovými vlastnostmi přeměňují elektrickou energii na tepelnou energii. Tyto prvky jsou rezistory. Vyznačují se elektrickým odporem, který se měří v ohmech (Ohm). Jejich symbol je na obr. 1.2.

Reaktivní prvky – prvky schopné akumulovat elektrickou energii a uvolňovat ji buď do zdroje, ze kterého byla tato energie přijata, nebo ji předávat jinému prvku. V žádném případě tento prvek nepřeměňuje elektrickou energii na tepelnou. Takovými prvky jsou induktor a kondenzátor. Na Obr. Obrázek 1.3 ukazuje symbol těchto reaktivních prvků.
Elektrický obvod je spojení elektrických prvků, při kterém vlivem zdroje elektrické energie protéká v prvcích elektrický proud.
Uzel – bod spojení tří nebo více prvků.
Větev – úsek řetězce obsahující alespoň jeden prvek a umístěný mezi dvěma nejbližšími uzly.
Obrys – uzavřená část elektrického obvodu.
Skokan je elektrický vodič s nulovým odporem, připojený na svých koncích ke dvěma různým bodům v obvodu.
Klasifikace elektrických obvodů se provádí podle následujících kritérií:
– přítomnost nebo nepřítomnost zdroje elektrické energie v obvodu;
– přítomnost nebo nepřítomnost disipativních prvků v řetězci;
– v závislosti na povaze charakteristik proudového napětí elektrických prvků;
– v závislosti na počtu svorek elektrického obvodu.
Pasivní obvod nazývá se obvod, který neobsahuje zdroj elektrické energie. V takovém řetězci jsou přítomny pouze disipativní a reaktivní prvky.
Aktivní obvod Nazývá se obvod obsahující alespoň jeden zdroj elektrické energie. Aktivní obvody zahrnují obvody obsahující zesilovací prvky – tranzistory a elektronky, protože jejich ekvivalentní obvody zahrnují zdroje elektrické energie.
Všechny pasivní a aktivní obvody se zase dělí na reaktivní a disipativní.
Reaktivní obvod nazývaný obvod obsahující pouze reaktivní prvky. V takových obvodech nejsou žádné disipativní prvky a reaktivní prvky jsou považovány za ideální.
Disipativní řetězec nazývá se řetězec obsahující alespoň jeden disipativní prvek. Může to být rezistor nebo skutečný reaktivní prvek. Je zřejmé, že ve skutečnosti jsou všechny řetězce disipativní. Často jsou však disipativní složky v reaktivních prvcích velmi malé a lze je zanedbat. To je však nutné pokaždé vyhodnotit a vyjednat.
Nakonec se všechny jmenované typy obvodů v závislosti na typu proudově-napěťové charakteristiky prvků dělí na lineární a nelineární.
Lineární Elektrický obvod je obvod obsahující pouze prvky s lineární charakteristikou proud-napětí.
Nelineární elektrický obvod je obvod obsahující alespoň jeden prvek s nelineární charakteristikou proud-napětí.
















