Planimetrie je obor geometrie, který studuje dvojrozměrné obrazce, tedy obrazce, které mohou být umístěny ve stejné rovině. Obrazce studované planimetrií: bod, úsečka, obdélník, čtverec, kruh atd.
Předměty, které nás obklopují, nejsou vždy ploché, častěji určitou část prostoru zabírají skutečné předměty.
Stereometrie je obor geometrie, ve kterém se studují postavy v prostoru. Obrazce studované stereometrií: krychle, koule, kužel, rovnoběžnostěn, pyramida atd.
Toto slovo (στερεομετρία) pochází ze starověkých řeckých slov „stereos“ – objemový, prostorový a „metria“ – rozměr.
Jsou-li povrchy geometrických těles složeny z mnohoúhelníků, pak se taková tělesa nazývají mnohostěny.
Fazety – Toto jsou mnohoúhelníky, které tvoří mnohostěn. Dvě sousední plochy nemohou ležet ve stejné rovině.
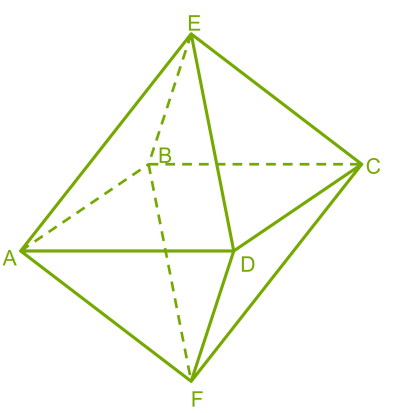
Konvexní mnohostěn se vyznačuje tím, že je umístěn na jedné straně roviny každé z jeho ploch. Na obrázku je znázorněn konvexní mnohostěn – osmistěn. Osmistěn má osm stěn, všechny stěny jsou pravidelné trojúhelníky.

Obrázek ukazuje nekonvexní (konkávní) mnohoúhelník. Pokud vezmeme v úvahu například rovinu trojúhelníku (EDC), pak je zjevně část mnohoúhelníku na jedné straně a část na druhé straně této roviny.
Pro další definice zavedeme pojem rovnoběžné roviny a rovnoběžné přímky v prostoru a kolmost přímky a roviny.
Dvě přímky v prostoru se nazývají rovnoběžné, pokud leží ve stejné rovině a neprotínají se.
Přímka se nazývá kolmá k rovině, pokud je kolmá k jakékoli přímce v této rovině.
(n)-gonální hranol je mnohostěn složený ze dvou stejných (n)-úhelníků ležících v rovnoběžných rovinách a (n)-rovnoběžek, které vznikly spojením vrcholů (n)-úhelníků se segmenty rovnoběžných čar.
U přímých hranolů jsou všechny boční plochy obdélníkové. Boční hrany přímého hranolu jsou kolmé k rovinám jeho podstav.
Je-li kolmice vedena z libovolného bodu jedné základny k jiné základně hranolu, pak se tato kolmice nazývá výška hranolu.


Obrázek ukazuje pravý trojúhelníkový hranol. Všechny boční plochy jsou obdélníky, kteroukoli boční hranu lze nazvat výškou hranolu. Trojúhelníkový hranol nemá žádné úhlopříčky, protože všechny vrcholy jsou spojeny hranami.

Na obrázku je vidět pravidelný čtyřboký hranol. Základy hranolu jsou čtverce. Všechny úhlopříčky pravidelného čtyřbokého hranolu jsou stejné, v jednom bodě se protínají a v tomto bodě půlí.

Obrázek ukazuje pravoúhlý rovnoběžnostěn. Délky tří hran se společným vrcholem se nazývají rozměry pravoúhlého rovnoběžnostěnu.
Protože trojúhelníky ABC a AC C 1 jsou pravoúhlé, pak se druhá mocnina délky úhlopříčky pravoúhlého rovnoběžnostěnu rovná součtu čtverců jeho rozměrů:
Pokud nakreslíte řez odpovídajícími úhlopříčkami podstav, dostanete to, co se nazývá diagonální řez hranolu.
U přímých hranolů jsou diagonální řezy obdélníky. Stejné diagonální sekce procházejí stejnými úhlopříčkami.

Na obrázku je vidět pravidelný šestiboký hranol, ve kterém jsou zakresleny dva různé diagonální řezy, které procházejí různě dlouhými úhlopříčkami.
1. Boční plocha S strana. = P základní ⋅ H, kde (H) je výška hranolu. U šikmých hranolů se plocha každé boční plochy určuje samostatně.
2. Kompletní povrch S kompletní. = 2 ⋅ S základ . + S strana. . Tento vzorec platí pro všechny hranoly, nejen pro rovné.
(n)-gonální jehlan je mnohostěn složený z (n)-úhelníku na základně a (n)-trojúhelníků, které jsou vytvořeny spojením vrcholového bodu jehlanu se všemi vrcholy základního mnohoúhelníku.

Jehlan, jehož základna je pravidelný mnohoúhelník a jehož výška spojuje vrchol jehlanu se středem pravidelného mnohoúhelníku, se nazývá pravidelný.
Pravidelná pyramida má všechny boční stěny stejné rovnoramenné trojúhelníky. Pokud nakreslíte výšky těchto trojúhelníků, budou také stejné.

Na obrázku je pravidelný čtyřboký jehlan. Výška jehlanu (KO) se kreslí od vrcholu (K) ke středu základny (O).
Pokud má pravidelná trojúhelníková pyramida všechny její boční strany rovnostranné trojúhelníky (rovné se základnou), pak se taková pyramida nazývá pravidelný čtyřstěn:

Pokud má mnohoúhelník na své základně úhlopříčky, pak lze těmito úhlopříčkami a vrcholem jehlanu nakreslit diagonální řez.

1. Boční plocha S strana. = P základní ⋅ h 2 , kde (h) je apotém. U jehlanů, které nejsou pravidelné, je nutné určit povrch každé boční plochy zvlášť.
2. Kompletní povrch S kompletní. = S základní + S strana. . Tento vzorec platí pro všechny pyramidy, nejen pro ty běžné.
3. Objem V = 1 3 ⋅ S základ. ⋅ H, kde (H) je výška pyramidy. Tento vzorec platí pro všechny pyramidy, nejen pro ty běžné.

V geometrii stupně 10 jsou sekce, které studují vlastnosti úhlopříčky pravoúhlého rovnoběžnostěnu. Vlastnosti jsou studovány z nějakého důvodu; mnoho problémů s nalezením úhlopříčky tohoto obrazce se nachází v jednotné státní zkoušce. Proto má smysl podrobně mluvit o vlastnostech úhlopříčky obdélníkového rovnoběžnostěnu.

Definice pojmu
Obecně platí, že úhlopříčka je segment spojující vrcholy dvou úhlů, které nepatří na stejnou stranu mnohostěnu. Obdélníkový rovnoběžnostěn se zase skládá ze šesti ploch, které jsou obdélníky.
Úhlopříčky v pravoúhlém rovnoběžnostěnu lze kreslit nejen ve vnitřním prostoru figury, ale také na bočních plochách a na základních plochách. V druhém případě se obvykle uvádí, že mluvíme o úhlopříčce bočního čela nebo úhlopříčce základny.
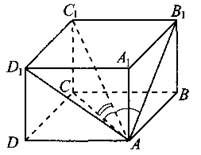
Rýže. 1. Úhlopříčky rovnoběžnostěnu.
Rovnoběžnostěn má čtyři úhlopříčky. Navíc tyto segmenty nepatří k žádné boční ploše nebo základně, ale jsou nakresleny uvnitř obrázku.
Diagonální charakteristiky
Existují dvě věty o úhlopříčkách rovnoběžníku. K jejich prokázání se používají doplňkové konstrukce. Například často úhlopříčka spodní základny daného objemového geometrického útvaru slouží jako strana pro několik trojúhelníků.
První věta
Čtverec úhlopříčky kvádru lze najít sečtením druhých mocnin tří rozměrů tohoto geometrického útvaru.
Zde hovoříme o délce, šířce a výšce dotyčného mnohostěnu. K prokázání této věty je nutné použít vlastnosti pravoúhlých trojúhelníků.
Úhlopříčka nakreslená na základně bude přepona pravoúhlého trojúhelníku $ABC$, což znamená, že ji lze najít pomocí Pythagorovy věty prostřednictvím součtu čtverců $AB$ a $BC$.
Dále zvažte pravoúhlý trojúhelník $ACC’$. Úhlopříčku $AC’$ lze také nalézt pomocí Pythagorovy věty jako kořen součtu nohou $AC$ a $CC’$. Ale již jsme našli $AC$ jako odmocninu součtu čtverců $AB$ a $AC$:
Takto vypadá vzorec, který odráží obsah této věty.
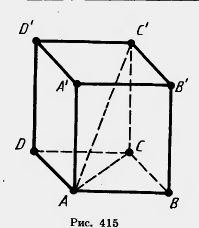
Rýže. 2. Spojení mezi úhlopříčkou kvádru a jeho okrajem a základnou.
Obvykle se za jeho délku považuje větší segment ležící u základny kvádru. Menší segment je šířka.
Druhá věta
V každém rovnoběžnostěnu se čtyři úhlopříčky protínají v jednom bodě, který se nazývá bod symetrie, a jsou jím půleny. Tato vlastnost je prokázána zvážením libovolných dvou úhlopříček a nakreslením odpovídajících segmentů.
Abychom dokázali tuto větu, musíme si pamatovat, že rovinu lze definovat dvěma protínajícími se přímkami. V uvažovaném případě má řez rovinou definovanou dvěma protínajícími se úhlopříčkami tvar obdélníku. A úhlopříčky obdélníku, jak víte, jsou rozděleny na polovinu průsečíkem.
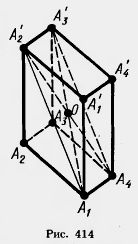
Rýže. 3. Průsečík kvádrových diagonál.
Ze stejné věty můžeme usoudit, že všechny její úhlopříčky budou stejné úsečky.
co jsme se naučili?
Mluvili jsme o úhlopříčkách kvádru. Dozvěděli jsme se, že pomocí vlastností úhlopříček rovnoběžnostěnu můžete zjistit šířku, délku a výšku kvádru. Mluvili jsme o tom, jak najít střed symetrie a určit délku úhlopříček pravoúhlého rovnoběžnostěnu.
















